Спрос на труд
3.1 Общие установки
3.2 Спрос на труд в краткосрочном периоде
3.2.1 В условиях конкуренции (1)
3.2.2 Монополия на рынке товаров (2)
3.2.3 Монополия на рынке труда (3)
3.2.4 Монополия плюс монопсония (4)
3.3 Спрос на труд в долгосрочном периоде в условиях конкуренции
3.3.1 Эффекты замещения и масштаба
3.3.2 Эластичность спроса на труд
3.3.3 Законы Маршалла-Хикса
3.3.4 Примеры
3.4 Альтернативный подход к построению функций спроса на труд
3.5 Теория эффективной зарплаты
3.1 Общие установки
- Фирмы - предприятия-покупатели рабочей силы, следовательно спрос на труд - производный спрос (зависит от ситуации на товарном рынке).
- Фирмы максимизируют прибыль π(L)
- издержки - И(L), зависят от количества (численности) работников, И(L) = w L + издержки других факторов производства
- доходы - Д(L) Д(L) = цена * объем продукции (выпуск) = p * f (L, ...)
цена p = α [выпуска]
"Альтернативные"
издержки - ценность лучшей упущенной возможности
- прибыль π(L) = Д(L) - И(L), требуется выбрать L так, чтобы максимизировать π
-
a) dπ/dL = 0 <=> dД/dL = RFm(L) = dИ/dL = CFm(L)
т. е. предельная доходность труда = предельным издержкам труда
если RFm(L) > CFm(L) , то выгодно нанимать еще одного работника
<=> d CFm(L)/dL > d RFm(L)/dL | 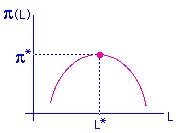 |
Структура рынков
По какой цене можно покупать труд и продавать (реализовывать) продукцию?
Зависят ли эти цены от поведения предприятия?
=> ответ связан с структурой рынков
| Рынок товаров | |||
| конкуренция | монополия | ||
| Рынок труда | конкуренция | 1 | 2 |
| монопсония | 3 | 4 | |
Сроки
- краткосрочный период
- в нем деятельность фирмы ограничена действующими контрактами, производственная технология неизменна
- долгосрочный период
- в нем деятельность фирмы не ограничена контрактами; технология, а также выпускаемая продукция могут изменяться
3.2 Спрос на труд в краткосрочном периоде
3.2.1 В условиях конкуренции на рынке товаров и на рынке труда (1)
Спрос одной фирмы
Конкуренция обозначает: фирма маленького размера по отношению к рынку (w, r, p - const).
- Доход: pY = p f(L,..),
где Y - выпуск, f(L,..) - производственная функция
- Расходы: wL + rk,
где rk - фиксированные издержки
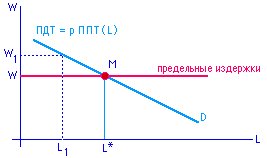
- Предельная доходность труда (ПДТ): RFm(L) = dД/dL = d [p f(L,..)] / dL = p f'(L)
f'(L) - предельная
производительность труда (ППТ),
(закон убывающей предельной производительности труда)
- Предельные издержки труда:
предельная производительность труда в денежном измерении
равна зарплате (предельным издержкам)
|
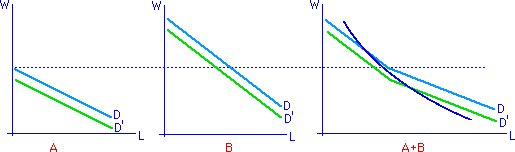
Как меняется кривая спроса?
p -> p', | 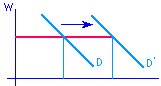 |
p f'(L) = w <=>
p = w/f'(L) = w / (dY/dL) = w dL/dY = dC/dY = Cm
3.2.2 Монополия на рынке товаров, конкуренция на рынке труда (2)
- Доход: Д = p Y
но: p = p(y)
- Предельный доход:
dД(y(L))/dL = (dД/dy) (dy/dL)
dy/dL = f'(L) - предельная
производительность труда (ППТ)
dД/dy = d[y p(y)] / dy = p(y) + y dp/dy =
p(y) [1 + (y/p) dp/dy]
εD/p = (dy/y) / (dp/p) = (p/y) dy/dp < 0
εD/p - эластичность спроса на производимый товар по цене
-
Предельная доходность труда (ПДТ):
RFm = p [1 + 1/εD/p] f'(L) = w где (1 + 1/εD/p ) < 1
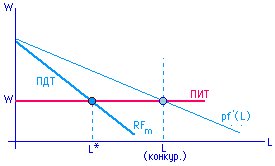
3.2.3 Монопсония на рынке труда, конкуренция на рынке товаров (3)
 |
Монопсония может быть:
|
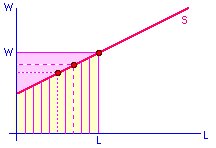
Недискриминирующая монопсония:
-
Издержки:
И = w(L) L
- Предельные издержки труда: dИ/dL = w(L) + L dw/dL
- CFm = w [1 + (L/w) dw/dL]
ηS/w = (dL/L) / (dw/w) = (w/L) dL/dw - эластичность предложения труда по зарплате
CFm = w [1 + 1/ηS/w ] где (1 + 1/ηS/w) > 1
3.2.4 Монополия на рынке товаров, монопсония на рынке труда (4)
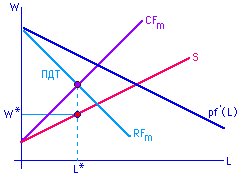
CFm = ПДТ => L = L*
W = W(L*)
= W* CFm = RFm
W(L) [1 + 1/ηS/w] = p f'(L) * [1 + 1/εD/p]
ηS/w > 0 - эластичность предложения труда по зарплате
3.3 Спрос на труд в долгосрочном периоде в условиях конкуренции
3.3.1 Эффекты замещения и масштаба
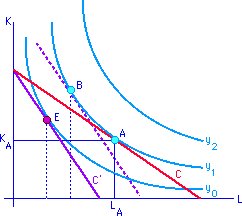 |
В долгосрочном периоде цены факторов не фиксированы. Допустим, растет заработная плата: C = wL + rKC' = w'L + rK w' > w
|
Возможно изменение технологии от А к В (пропорции K/L)
- технология (А): ресурсы LA и KA
- технология (B): более капиталоемкая
A -> B эффект замещения B -> E эффект масштаба
Условие максимизации прибыли:
(δY/δL) / (δY/δK) = MCL / MCK = w / r
3.3.2 Эластичность спроса на труд
Коэффициент эластичности спроса на труд по зарплате:
εL/w = (dL/L) / (dw/w) = (w/L) dL/dw
εL/w < -1 - спрос эластичен => увеличение w снижает занятость в большей степени, совокупный фонд зарплаты (Ф) снижается
Ф = L(w) w
dФ/dw = L(w) + w (dL/dw) = L[1 + (w/L) (dL/dw)] =L[1 + εL/w] <=>
εL/w < -1 => dФ/dw < 0
εL/w > -1 => dФ/dw > 0
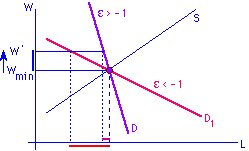
- D - спрос неэластичен: при подьеме w немногие теряют работу
- D1 - спрос эластичен: при подьеме w многие теряют работу
Возможность воздействия профсоюзов на зарплату зависит от эластичности спроса.
3.3.3 Законы Маршалла-Хикса (законы производного спроса)
Эластичность спроса на труд тем выше, чем выше
- эластичность спроса на товар
- доля трудовых издержек в совокупных издержках
- возможность замещения труда капиталом
- эластичность предложения других факторов производства
Пример: пусть p = aw + br => L = ay K = by
факторы K и L комплементарны,
r - цена капитала (const),
a и b
- фиксированы,
w - меняется
и рассматривается долгосрочное равновесие
<=> цена = средним издержкам
dp = a dw
dp/p = (aw/p) dw/w = νL dw/w
где νL = aw/p - доля зарплаты в цене продукции
Эластичность спроса на товар по цене:
εD/p = (dy/y) / (dp/p) =>
dy/y = εD/p νL dw/w
Но dL/L = dy/y (при фиксированном капитале) =>
dL/L = εD/p νL dw/w
следовательно эластичность спроса на труд по зарплате
εL/w = ε D/p νL
- Почему снизилась активность профсоюзов?
В связи с развитием международной торговли расширилась
конкуренция на рынке товаров => рост эластичности спроса на
товар => рост эластичности спроса на
труд => добиваться роста зарплаты можно только значительно
сокращая занятость => активность профсоюзов снижается
( 1-й закон
Маршалла-Хикса)
- Почему летчики получают такую высокую зарплату?
- доля зарплаты летчиков в совокупных издержках авиакомпаний ничтожно мала ( 2-й закон Маршалла-Хикса)
- летчиков нельзя заменить машинами, т.к. численность экипажа современных авиалайнеров уже сокращена до минимума ( 3-й закон Маршалла-Хикса)
=> эластичность спроса на труд летчиков низкая
=> они могут легко добиваться роста зарплаты
- Чем занимаются профсоюзы текстильной промышленности города Нью-Йорк?
=> высокая эластичность спроса на труд текстильных рабочих в Нью-Йорке
- высокая конкуренция со стороны других стран, производящих текстиль (азиатские страны, Великобритания) ( 1-й закон Маршалла-Хикса )
- конкуренция со стороны приезжих рабочих, желающих работать в Нью-Йорке ( 3-й закон Маршалла-Хикса , фактор-субститут)
=> профсоюзы борются не за рост зарплаты, а за сохранение численности занятых
3.4 Альтернативный подход к построению функций спроса на труд
Инверсия, или "перевернутая" производственная функция
спроса фирмы в краткосрочном периоде:
Q = Q (L, K)
при фиксированном K =
Kf => Q = Q (L, Kf)
и предполагается
существование обратной функции => L = L (Q)
Форма функции L(Q) зависит, таким образом, от технологии, т.е. от вида производственной функции Q(L,K)
Пример:
Qt = A Ltα Ktβ eθ t
A > 0, α> 0, β> 0, θ> 0 - параметры
eθ t - компонента тренда, улавливающая сдвиги в производственной функции в результате научно-технического прогресса
ln Qt = a + αln Lt + βln Kt + θt
ln Lt* = ao + a1 ln Qt + a2 ln Kt + a3 t
a = ln A; ao = -a/α; a1 = 1/α; a2 = -β/α; a3 = -θ/α;
Таким образом "желаемое" количество труда Lt* позитивно связано с уровнем выпуска, негативно - с количеством применяемого капитала и временным трендом.
Принимая во внимание практические трудности с измерением объема капитала, его приращение, как и научно-технический прогресс, можно учитывать с помощью временного тренда. Тогда модель принимает еще более простой вид:
ln Lt* = βo + β1 ln Qt + β2 t
Подобные функции применяются при прогнозировании спроса на труд.
3.5 Теория эффективной зарплаты
Усложнение базовой модели спроса - предположение о влиянии зарплаты на продуктивность труда. Тогда f'(L) (или ППТ) зависит от уровня w.
Модель эффективной зарплаты
Пусть e(w) - функция
усилия, e'(w) > 0
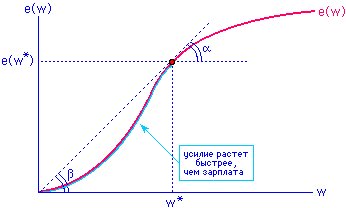
Наниматель, максимизируя прибыль, сам устанавливает уровень зарплаты (а не только занятости).
Пусть E - эффективная рабочая сила
E = e(w) L, где L - количество человеко-часов
найдем max π = max [ f (E) - w L ] по w, L
π = f ( e(w) L ) - w L =>
δπ/ δ L = δf/δ E * δE/δ L - w = 0
δπ/ δ w = δf/δ E * δE/δ w - L = 0
или
δf/δE * e(w) = w
δf/δE * δe(w) /δ w * L - L = 0
откуда получим
w / e(w) = 1 / (δe(w) / δw) =>
(δe(w) / e(w) ) / (δw / w ) = 1 (условие Солоу)
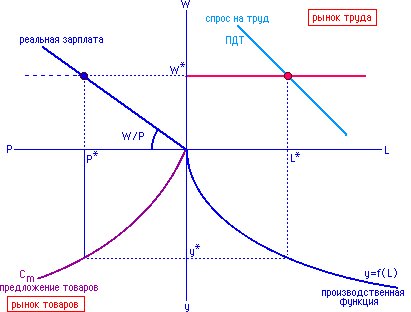
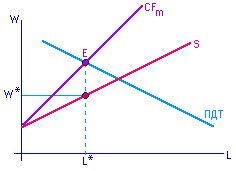
Эффективная зарплата устанавливается в точке, где эластичность усилия по зарплате равна единице. При этом w* может оказаться и выше равновесного рыночного уровня.
Практика установления зарплаты выше равновесного значения некоторыми экономистами расценивается как причина растущей безработицы. Это не всегда верно, т. к. рост продуктивности сдвигает кривую спроса вправо/вверх.
В результате при росте зарплаты от w1 до w3 занятость сокращается не до величины L4 , а до L3 (т. е. не так значительно).
Нашли опечатку?
Выделите её, нажмите Ctrl+Enter и отправьте нам уведомление. Спасибо за участие!
Сервис предназначен только для отправки сообщений об орфографических и пунктуационных ошибках.